Answer:
Volume of water required to fill the pyramid is
 rd of the water required to fill the prism completely.
rd of the water required to fill the prism completely.
Explanation:
Let Mr Jackson has an empty rectangular pyramid and rectangular prism.
Height and base of both are congruent.
So volume of rectangular pyramid
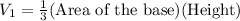
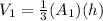
Volume of the rectangular prism = (Area of the base)(height)
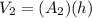
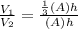 [ Since
[ Since
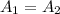 ]
]

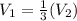
Therefore, amount of water required to fill the pyramid is
 rd of the water required to fill the prism completely.
rd of the water required to fill the prism completely.