Answer:
120.41 miles.
Explanation:
Given:
A is 90 miles from town B and 18 miles from town C-
Town a B and C are forming a right triangle at a a road connecting Town B and C directly.
Question asked:
Find the length of the road that means longest side of the triangle, BC = ?
Solution:
AB = 90 miles
AC = 80 miles
BC = ?
As we know:
By Pythagoras Theorem:
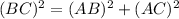
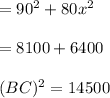
Taking root both sides;
![\sqrt[2]{(BC)^(2) } =\sqrt[2]{14500} \\ \\ BC=120.41\ miles](https://img.qammunity.org/2021/formulas/mathematics/middle-school/yw8yz62595qmmmk9bpnnudplbdovkxngfb.png)
Thus, length of the road is 120.41 miles.