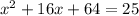Question

Monica is solving a quadratic equation. She wants to find the value of x by taking the square root of both sides of the equation. Which equation allows her to do this?

Answer 1

`x^(2) +16x+64=25`

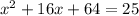
Explanation:

The options for this question are missing, the options are:

`x^(2) -10x-25=14\\x^(2) +160x+26=19\\x^(2) +16x+64=25\\x^(2) -9x+81=34`

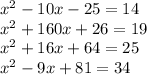
Monica want to solve a quadratic equation by taking the square root of both sides of the equation. To figure out if she can take the root of the left side of the equations given, she needs to see which one of them is the square of a binomial.

A square of a binomial has this form:

`(a+b)^(2) =a^(2) +2ab+b^(2) \\or\\(a-b)^(2) =a^(2) -2ab+b^(2)`

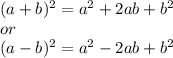
Looking at the options we have we can see that
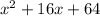`x^(2) +16x+64` is the square of the binomial
`(x+8)^(2)` (since 64 is the square of the second term and 16x would be the result of multiplying x by 8 by 2 like the second term in the previous formula).

Therefore,
`x^(2) +16x+64 =25` can be written as

`x^(2) +16x+64 =25\\(x+8)^(2) =25`

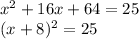
And now, we can take the square root of both side of the equation and solve for x:

`(x+8)^(2) =25\\(x+8)=5 \\x=5-8\\x=-3and \\(x+8)=-5\\x=-5-8\\x=-13`

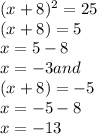
Thus, the right answer, and the equation that allows Monica to solve it by taking the square root of both sides of the equation is
`x^(2) +16x+64=25`

Answer 2

c) x^2 +16x + 64 = 25

Completed question;

Monica is solving a quadratic equation. She wants to find the value of x by taking the square root of both sides of the equation. Which equation allows her to do this?

a) x^2 - 10x - 25 = 14

b)x^2 + 160x +26 = 19

c) x^2 +16x + 64 = 25

d) x^2 - 9x + 81 = 34

Explanation:

To solve a quadratic equation by taking the square root of both sides, we should be able to express the equation in the form;

(x + a)^2 = b^2

Or

(x - a)^2 = b^2

From the above options,

Option C looks to give the desired form

x^2 + 16x + 64 = 25

Which can be further factorised as;

(x + 8)^2 = 5^2

(Note: a = 8 and b = 5)

square root of both sides;

x + 8 = +/- 5

x = +5-8 = -3 (solved)

or

x = -5-8 = -13 (solved)