Answer:
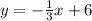
Explanation:
Slope-intercept form:
 , where
, where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.
The formula to find the slope of a line is
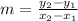 .
.
1) Plug the coordinates into this
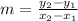 .
.
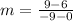
2) Solve it. Simplify it if possible.
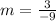
Simplified:
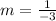
3) Plug the result into
 .
.
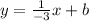
4) Plug one of the points (
 or
or
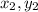 ) into
) into
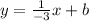 to find
to find
 .
.
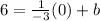
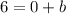
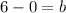

5) Plug the result of
 into
into
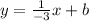 .
.
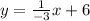
The negative situated in the denominator can be genaralised to the fraction.
Therefore,
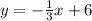 .
.