Question

Please show step by step solution

It is known that the population variance equals 484. With a 0.95 probability, the sample size that needs to be taken if the desired margin of error is 5 or less is


25


74


189


75

Answer 1

b) 74

The sample size that needs to be taken if the desired margin of error is 5 or less is 74

Step-by-step explanation:

Step-by-step explanation:-

Given population variance σ² = 484

σ = √484

σ = 22

The level of significance ∝=0.95

The z-score of 0.95 level of significance = 1.96

Given Margin of error = 5

we know that the margin of error is determined by

`M.E = (Z_(\alpha )S.D )/(√(n) )`

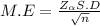
cross multiplication, we get

`√(n) = (Z_(\alpha )S.D )/(M.E)`

`√(n) = (1.96 X22 )/(5) = 8.624`

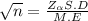
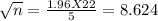
Squaring on both sides, we get

n = (8.624) ²

n = 74.37 ≅74

Conclusion:-

The sample size that needs to be taken if the desired margin of error is 5 or less is 74