Question

Problem PageQuestion

Suppose that the heights of adult women in the United States are normally distributed with a mean of 65 inches and a standard deviation of 2.4 inches. Jennifer is taller than 70% of the population of U.S. women. How tall (in inches) is Jennifer? Carry your intermediate computations to at least four decimal places. Round your answer to one decimal place.

Answer 1

Jennifer is 66.3 inches tall; this is calculated by finding the z-score for the 70th percentile and using it with the mean and standard deviation of the population.

Step-by-step explanation:

To determine how tall Jennifer is, given that she is taller than 70% of the population of U.S. women, we need to find the corresponding z-score that reflects the 70th percentile of a normal distribution, and then use it to calculate her height.

Firstly, using a standard normal distribution table or a calculator, we find the z-score that corresponds to the 70th percentile. Generally, this z-score is around 0.5244 (this can vary slightly depending on the table or technology used to find it). Now we apply the formula for converting a z-score to the actual score using the population mean and standard deviation:

Height = mean + (z-score × standard deviation)

Plugging in the values for the population mean and standard deviation:

Height = 65 + (0.5244 × 2.4)

Height = 65 + 1.2586

Height = 66.2586 inches

After rounding, we conclude that Jennifer is 66.3 inches tall.

Answer 2

Jennifer's height is 63.7 inches.

Step-by-step explanation:

Let X = heights of adult women in the United States.

The random variable X is normally distributed with mean, μ = 65 inches and standard deviation σ = 2.4 inches.

To compute the probability of a normal random variable we first need to convert the raw score to a standardized score or z-score.

The standardized score of a raw score X is:

`z=(X-\mu)/(\sigma)`

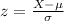
These standardized scores follows a normal distribution with mean 0 and variance 1.

It is provided that Jennifer is taller than 70% of the population of U.S. women.

Let Jennifer's height be denoted by x.

Then according to the information given:

P (X > x) = 0.70

1 - P (X < x) = 0.70

P (X < x) = 0.30

⇒ P (Z < z) = 0.30

The z-score related to the probability above is:

z = -0.5244

*Use a z-table.

Compute the value of x as follows:

`z=(X-\mu)/(\sigma)`

`-0.5244=(x-65)/(2.4)`

`x=65-(0.5244* 2.4)`

`=63.7414\\\approx63.7`

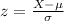
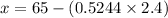
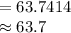
Thus, Jennifer's height is 63.7 inches.