Answer:
154 cm
Explanation:
We are given that
Area of rectangle=A=96 square cm
We have to find the difference between the greatest and least perimeter of the rectangles.
Let
Length of rectangle,l=x
Breadth of rectangle.b=y
Area of rectangle=
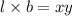

Factors of 96 are
1,2,3,4,6,8,12,16,24,32,48,96
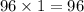
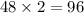
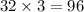
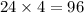
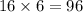
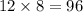
Perimeter of rectangle,P=
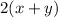
When x=96 an y=1
P=
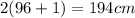
When x=48 and y=2
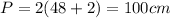
When x=24 and y=4
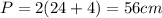
When x=16 and y=6
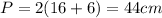
When x=12 and y=8

When x=32 and y=3

Greatest perimeter of rectangle=194 cm
Least perimeter of rectangle=40 cm
Difference between the greatest and least perimeter of the rectangles=194-40=154 cm