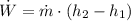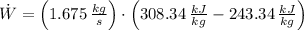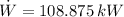Question

Refrigerant 134a enters an insulated compressor operating at steady state as saturated vapor at -12oC with a volumetric flow rate of 0.18 m3/s. Refrigerant exits at 7 bar, 70oC. Changes in kinetic and potential energy from inlet to exit can be ignored. Determine the volumetric flow rate at the exit, in m3/s, and the compressor power, in kW.

Answer 1

`\dot V_(out) = 0.061\,(m^(3))/(s)`,
`\dot W = 108.875\,kW`

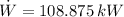
Step-by-step explanation:

The process in the compressor is modelled after the First Law of Thermodynamics:

`\dot W + \dot m \cdot (h_(1)-h_(2)) = 0`

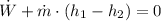
The specific enthalpies of the refrigerant at inlet and outlet are, respectively:

Inlet (Saturated vapor)

`\\u = 0.10744\,(m^(3))/(kg)`

`h = 243.34\,(kJ)/(kg)`

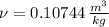
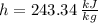
Outlet (Superheated Vapor)

`\\u = 0.036373\,(m^(3))/(kg)`

`h = 308.34\,(kJ)/(kg)`

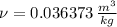
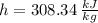
The mass flow is:

`\dot m = (\left(0.18\,(m^(3))/(s) \right))/(0.10744\,(m^(3))/(kg) ) \co`

`\dot m = 1.675\,(kg)/(s)`

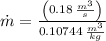
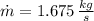
The volumetric flow rate at the exit is:

`\dot V_(out) = \left(1.675\,(kg)/(s) \right)\cdot \left(0.036373\,(m^(3))/(kg) \right)`

`\dot V_(out) = 0.061\,(m^(3))/(s)`

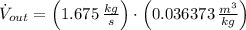
The power needed to make the compressor work is:

`\dot W = \dot m \cdot (h_(2)-h_(1))`

`\dot W = \left(1.675\,(kg)/(s) \right)\cdot \left(308.34\,(kJ)/(kg)-243.34\,(kJ)/(kg) \right)`

`\dot W = 108.875\,kW`