Answer:
Confidence = 0.94 = 94%
Explanation:
Solution:-
- A 99% confidence interval (in inches) for the mean height of a population is:
65.44 < μ < 66.96
- If the confidence interval is obtained from the same sample data:
65.65 < μ < 66.75
- The sample size, n = 144
- You will first need to find the sample mean (x_bar) and sample standard deviation (s) based on the confidence interval given. The width of the confidence interval is 2E
2E = 66.96-65.44 = 1.52
E = 0.76
- The test statistic error (E) is defined as:
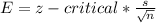
Where, Z-critical for 99% confidence = 2.5758
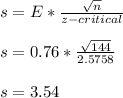
- Since,
x_bar - E = 65.44
x_bar = 65.44 - 0.76 = 66.2
- Use the value you found in part a to determine the degree of confidence for the interval 65.65 < μ < 66.75 is based on:
66.2 - E = 65.65
E = 0.55
- The test statistic error (E) is defined as:
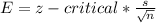
- Determine the Z-critical value from equation above:
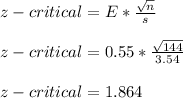
- The level of confidence for the corresponding Z-critical value would be:
Confidence = P ( - z-critical < Z < z-critical )
Confidence = P ( - 1.864 < Z < 1.864 )
Confidence = 0.94 = 94%