Answer:
100m+n = 6425
Explanation:
Let X be the book Velma picks and Y the book that Daphne picks. Note that X and Y are independent and identically distributed, so for computations, i will just focus on X for now.
Lets denote with A, B, C and D the books with 200, 400, 600 and 800 pages respectively.
Note that, without any restriction P(X=A) = P(X=B) = P(X=C) = P(X=D) = 1/4. However, if we also add the condition that R = 122, where R is the page picked, we will need to apply the Bayes formula. For example,
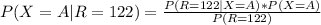
P(X=A) is 1/4 as we know, and the probability P(R=122|X=A) is basically the probability of pick a specific page from the book of 200 pages long, which is 1/200 (Note however, that if he had that R were greater than 200, then the result would be 0).
We still need to compute P(R=122), which will be needed in every conditional probability we will calcultate. In order to compute P(R=122) we will use the Theorem of Total Probability, in other words, we will divide the event R=122 in disjoint conditions cover all possible putcomes. In this case, we will divide on wheather X=A, X=B, X=C or X=D.

Thus, P(R=122) = 1/396
With this in mind, we obtain that
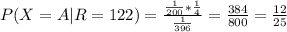
In a similar way, we can calculate the different values that X can take given that R = 122. The computation is exactly the same except that for example P(R=122|X=B), is 1/400 and not 1/200 because B has 400 pages.
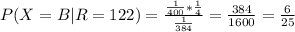
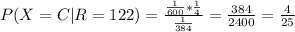

We can make the same computations to calculate the probability of Y = A,B,C or D, given that R=304. However, P(Y=A|R=304) will be 0 because A only has 200 pages (similarly, P(R=304|Y=A) = 0, R=304 and Y=A are not compatible events). First, lets compute the probability that R is 304.
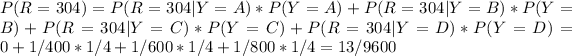
Thus, P(R=304) = 13/9600. Now, lets compute each of the conditional probabilities
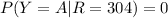 (as we stated before)
(as we stated before)
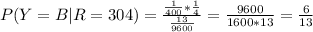
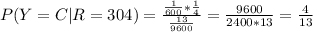
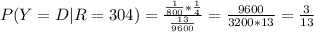
We want P(X=Y) given that
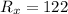 and
and
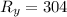 (we put a subindex to specify which R goes to each variable). We will remove the conditionals to ease computations, but keep in mind that we are using them. For X to be equal to Y there are 3 possibilities: X=Y=B, X=Y=C and X=Y=D (remember that Y cant be A given that
(we put a subindex to specify which R goes to each variable). We will remove the conditionals to ease computations, but keep in mind that we are using them. For X to be equal to Y there are 3 possibilities: X=Y=B, X=Y=C and X=Y=D (remember that Y cant be A given that
![R_y = 304). Using <strong>independence</strong>, we can split the probability into a multiplication.</p><p>[tex] P(X=Y=B) = P(X=B|R=122)*P(Y=B|R=304) = (6)/(25) * (6)/(13) = (36)/(325)]()
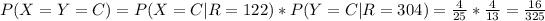

Therefore

61 is prime and 325 = 25*13, thus, they are coprime. Therefore, we conclude that m = 61, n = 325, and thus, 100m+n = 6425.