Question

A billiard ball is moving in the x-direction at 30.0 cm/s and strikes another billiard ball moving in the y-direction at 40.0 cm/s. As a result of the collision, the first ball moves at 50.0 cm/s, and the second ball stops. What is the change in kinetic energy of the system as a result of the collision

Answer 1

Step-by-step explanation:

Given that,

Initial speed of the billiard ball 1, u = 30i cm/s

Initial speed of another billiard ball 2, u' = 40j cm/s

After the collision,

Final speed of first ball, v = 50 cm/s

Final speed of second ball, v' = 0 (as it stops)

Let us consider that both balls have same mass i.e. m

Initial kinetic energy of the system is :

`K_i=(1)/(2)mu^2+(1)/(2)mu'^2\\\\K_i=(1)/(2)m(u^2+u'^2)\\\\K_i=(1)/(2)m((30)^2+(40)^2)\\\\K_i=1250m\ J`

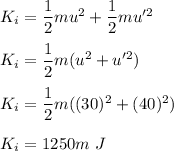
Final kinetic energy of the system is :

`K_f=(1)/(2)mv^2+(1)/(2)mv'^2\\\\K_f=(1)/(2)m(v^2+v'^2)\\\\K_f=(1)/(2)m((50)^2+(0)^2)\\\\K_f=1250m\ J`

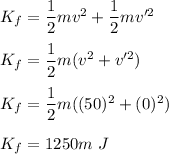
The change in kinetic energy of the system is equal to the difference of final and initial kinetic energy as :

`\Delta K=K_f-K_i\\\\\Delta K=1250m-1250m\\\\\Delta K=0`

So, the change in kinetic energy of the system as a result of the collision is equal to 0.