We have been given an equation
 . We are asked to fill in the blanks using our given equation.
. We are asked to fill in the blanks using our given equation.
The axis of symmetry will be the vertical line passing through vertex.
First of all, we will convert our given equation in standard vertex form of parabola as:
Standard vertex form of parabola:
 , where (h,k) is vertex of parabola.
, where (h,k) is vertex of parabola.
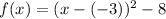
Upon comparing our function with standard vertex form, we can see that vertex of parabola is at
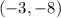 .
.
The axis of symmetry will be vertical line passing through point
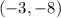 . The vertical line will pass through
. The vertical line will pass through
 , therefore, the axis of symmetry is
, therefore, the axis of symmetry is
 .
.
Since our given parabola is an upward opening parabola, so it has a minimum at
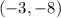 . This means that parabola will intersect the x-axis at two points. Therefore, there are two real solutions for the given function.
. This means that parabola will intersect the x-axis at two points. Therefore, there are two real solutions for the given function.