Question

A computer program has a bug that causes it to fail once in every thousand runs, on average. In an effort to find the bug, independent runs of the program will be made until the program has failed six times. What is the standard deviation of the number of runs required?

Answer 1

The standard deviation of the number of runs required is 2447.26

Explanation:

For each run, there are only two possible outcomes. Either the program fails, or it does not. The probability of the computer failing during a run is independent of other runs. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The standard deviation for the expected number of trials for r sucesses is:

`√(V(X)) = \sqrt{(r(1-p))/(p^(2))}`

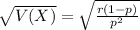
A computer program has a bug that causes it to fail once in every thousand runs, on average.

This means that
`p = (1)/(1000) = 0.001`

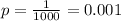
In an effort to find the bug, independent runs of the program will be made until the program has failed six times. What is the standard deviation of the number of runs required?

This means that r = 6. So

`√(V(X)) = \sqrt{(6*0.999)/((0.001)^(2))} = 2447.26`

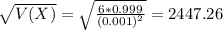
The standard deviation of the number of runs required is 2447.26