Question

What is the value of x if the volume of the cone is 12 pi m3

Answer 1

1. 130 2/3 ft3

2. 226 in.3

3. 33 cm3

4. 4 m

5. 15 m

Answer 2

Height of the cone = 4 m

Explanation:

Given:

Volume of a cube = (12π) m^3

Radius of the cone = (6/2) m = 3 m

We have to find the value of "x".

And "x" is the height of the cone from the figure shown.

Formula to be used:

Volume of the cone: 1/3(πr^2h)

Here height = "x"

⇒
`V_c_o_n_e=(\pi r^2 h)/(3)`

⇒
`V_c_o_n_e=(\pi r^2 x)/(3)`

⇒
`3* V_c_o_n_e=(\pi r^2 x)/(3)* 3`

⇒
`3* V_c_o_n_e=\pi r^2 x`

⇒
`(3* V_c_o_n_e)/(\pi r^2) =(\pi r^2* x)/(\pi r^2)`

⇒
`x=(3* V_c_o_n_e)/(\pi r^2 )`

⇒
`x=(3* 12\pi )/(\pi (3)^2 )`

⇒
`x=(36\pi )/(9\pi )`

⇒
`x=(36)/(9)`

⇒
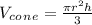
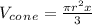
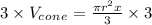
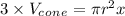
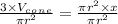
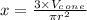
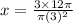
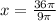
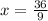
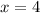`x=4` meters.

The height of the cone "x" = 4 meters option A is the right choice.