Question

A computer is inspected at the end of every hour. It is found to be either working (up) or failed (down). If the computer is found to be up, the probability of its remaining up for the next hour is 0.9. If it is down, the computer is repaired, which may require more than 1 hour. Whenever the computer is down (regardless of how long it has been down), the probability of its still being down 1 hour later is 0.75.a) Construct the (one-step) transition matrix for this Markov chain.

b) What is the long-term fraction of downtime of the computer?

c) If the computer is working right now, what is the probability that it will be down 10 hours from now?

Answer 1

a) Transition matrix:

`\left[\begin{array}{ccc}0.90&0.10\\0.25&0.75\end{array}\right]`

b) The long-term fraction of downtime of the computer is 0.286 or 28.6%.

c) The probability of being down 10 hours from now is independent of the inital state and is equal to 0.286.

Explanation:

We have two states for the computer: Up and Down.

The rows will represent the actual state and the column the next state, and the numbers within the matrix will be the probabilities of transition from the state of the row to the state of the column.

- If the computer is Up, there is a probability of 0.9 of being Up in the next hour. Then, there is a probability of 0.1 of being Down in the next hour.

- If the computer is Down, there is a probability of 0.75 of being Down in the next hour. Then, there is a probability of 0.25 of being Up in the next hour.

a) The transition matrix becomes:

`\left[\begin{array}{ccc}&U&D\\U&0.90&0.10\\D&0.25&0.75\end{array}\right]`

b) We can consider that we have a long-term state (stable) [πU, πD] when the fraction of each state does not change. This can be expressed as:

`\left[\begin{array}{ccc}\pi_U&\pi_D\end{array}\right] *\left[\begin{array}{ccc}0.90&0.10\\0.25&0.75\end{array}\right]=\left[\begin{array}{ccc}\pi_U&\pi_D\end{array}\right]`

If we develop this multiplication of matrix we get:

`0.90\pi_U+0.25\pi_D=\pi_U\\\\0.10\pi_U+0.75\pi_D=\pi_D`

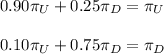
As this equations are linear combinations of each other, we need another equation to solve this.

We also know that the sum of the fractions of uptime and downtime is equal to one.

Solving these equation, we can calculate the long-term downtime fraction:

`0.90\pi_U+0.25\pi_D=\pi_U\\\\0.25\pi_D=(1-0.90)\pi_U=0.10\pi_U\\\\\pi_U=(0.25/0.10)\pi_D=2.5\pi_D\\\\\\\pi_D+\pi_U=1\\\\\pi_D+2.5\pi_D=1\\\\3.5\pi_D=1\\\\\pi_D=1/3.5=0.286`

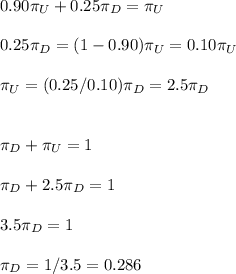
The long-term fraction of downtime of the computer is 0.286 or 28.6%.

c) To know what is the probability that it will be down 10 hours from now if the computer is now on, we have to compute the transition matrix for 10 hours. This is:

`T^(10)=\left( \left[\begin{array}{ccc}0.90&0.10\\0.25&0.75\end{array}\right]\right)^(10)= \left[\begin{array}{ccc}0.714&0.286\\0.714&0.286\end{array}\right]`

This is considered a steady state already.

If the computer is up, the actual state is [1, 0].

If we multiply this by the transition matrix, we get:

`\left[\begin{array}{ccc}1&0\end{array}\right] *\left[\begin{array}{ccc}0.714&0.286\\0.714&0.286\end{array}\right]=\left[\begin{array}{ccc}0.714&0.286\end{array}\right]`

The probability of being down 10 hours from now is independent of the inital state and is equal to 0.286.