Question

Mr. Black is flying a kite above a field on a 65 foot string. The angle of elevation of the kite is 70 degrees. How high is the kite above Mr. Black's head? (3 pts.)

Answer 1

The correct answer is 61.08 foot.

Explanation:

Length of the string of the kite, Mr. Black is flying is 65 foot. Thus the length between the kite and Mr. Black is given by 65 foot.

Angle of elevation is 70°.

We need to calculate the height of the kite above Mr. Black's head. The height is given by finding the sine of the angle of elevation.

Let the height be x foot.

Thus sin 70° =
`(x)/(65)`

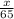
⇒ x = sin 70° × 65

⇒ x = 61.08

Thus the height of the kite above Mr. Black head is 61.08 foot.