Question

A laser beam is incident at an angle of 29.8° to the vertical onto a solution of corn syrup in water. (a) If the beam is refracted to 18.62° to the vertical, what is the index of refraction of the syrup solution? (b) Suppose the light is red, with wavelength 632.8 nm in a vacuum. Find its wavelength in the solution.

Answer 1

(a) 1.5

(b)
`421.86 * 10^(-9) m`

Step-by-step explanation:

Angle of incidence,
`i` = 29.8°

Angle of refraction,
`r` = 18.62°

(a) Index of refraction is given as:

`n = (sin(i))/(sin(r))`

`n = (sin(29.8))/(sin(18.62)) \\\\\\n = (0.4970)/(0.3193) \\\\\\n = 1.5`

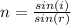
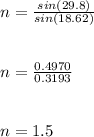
The refractive index of the syrup is 1.5.

(b) Wavelength of the red light in a vacuum, λ(1) =
`632.8 nm = 632.8 * 10^(-9) m`

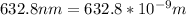
Refractive index is also a ratio of the speed of the light in a vacuum with the speed of light in a particular medium:

`n = (c)/(v)`

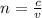
The speed of light in a vacuum is given as;

c = λ(1) * f

=> f = c/λ(1)

The speed of light in a medium is given as;

v = λ(2) * f

=> f = v/λ(2)

(λ = wavelength and f = frequency)

We know that the frequency of light does not change when it changes media, hence, we can equate both frequencies:

c/λ(1) = v/λ(2)

Therefore:

c / v = λ(1) / λ(2)

Therefore, refractive index will become:

n = λ(1) / λ(2)

=> 1.5 =
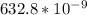`632.8 * 10^(-9)` / λ(2)

The wavelength of the red light in the solution is therefore:

λ(2) =
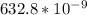`632.8 * 10^(-9)` / 1.5

λ(2) =
`421.86 * 10^(-9) m`

The wavelength of the light in the solution is
`421.86 * 10^(-9) m`