Answer:
The average induced emf around the border of the circular region is
 .
.
Step-by-step explanation:
Given that,
Radius of circular region, r = 1.5 mm
Initial magnetic field, B = 0
Final magnetic field, B' = 1.5 T
The magnetic field is pointing upward when viewed from above, perpendicular to the circular plane in a time of 125 ms. We need to find the average induced emf around the border of the circular region. It is given by the rate of change of magnetic flux as :
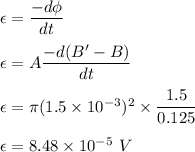
So, the average induced emf around the border of the circular region is
 .
.