Question

Spring break can be a very expensive holiday. A sample of 80 students is surveyed, and the average amount spent by students on travel and beverages is $593.84. The sample standard deviation is approximately $369.34. Is $521.58 ≤μ≤ $666.10 correct?

Answer 1

$521.58 < μ < $666.1

Explanation:

Spring break can be a very expensive holiday. A sample of 80 students is surveyed, and the average amount spent by students on travel and beverages is $593.84 at 92% confidence level. The sample standard deviation is approximately $369.34. Is $521.58 ≤μ≤ $666.10 correct?

Given that:

number of samples (n) = 80 students, mean (μ) = $593.84, standard deviation (σ) = $369.34, confidence level (c) = 92% = 0.92.

α = 1 - c = 1 - 0.92 = 0.08

`(\alpha )/(2) =(0.08)/(2) = 0.04`

the z score of 0.46 (0.5 - 0.04) is the same as the z score of 0.04. This is gotten from the Normal Distribution Table.

Therefore,
`z_{(\alpha )/(2) }=z_(0.04)=1.75`

The margin of error (e) is given as:

`e=z_(0.04)(\sigma)/(√(n) )=1.75*(369.34)/(√(80) ) =72.26`

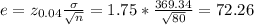
The confidence interval = (μ - e, μ + e) = ($593.84 - $72.26, $593.84 + $72.26) = ($521.58, $666.1)

The confidence interval is $521.58 < μ < $666.1