Question

A manufacturer of brand A jeans has daily production costs of Upper C equals 0.3 x squared minus 114 x plus 11 comma 405​, where C is the total cost​ (in dollars) and x is the number of jeans produced. How many jeans should be produced each day in order to minimize​ costs? What is the minimum daily​ cost?

Answer 1

190 Jeans

Explanation:

The daily production cost of the jeans manufacturer is given as:

`C=0.3x^2-114x+11405`

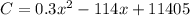
To determine the number of Jeans,x that should be produced daily to minimize cost, C. We take the derivative of C and solve for its critical points.

`C'=0.6x-114\\$When C'=0\\0.6x-114=0\\0.6x=114\\x=190`

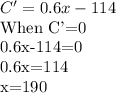
Therefore, to minimize daily cost, 190 Jeans is the number of jeans that should be produced daily.