Question

A particle starts at point A on the positive x-axis at time t = 0 and travels along the curve from A to B to C to D, as shown above. The coordinates of the particle's position (x(t), y(t)) are differentiable functions of t, where x′(t)=dxdt=−9cos(πt6)sin(πt+1√2) and y′(t)=dydt is not explicitly given. At time t = 9, the particle reaches its final position at point D on the positive x-axis. The slope of the curve is undefined at point B. At what time t is the particle at point B?

Answer 1

the particle is at point B at t = 3 s

Explanation:

Solution:-

- The coordinates of the path that a particle follows through points A to B to C.

- The coordinates of the particle position ( x , y ) are differentiable function of t, where, the rate of change of x-coordinate is given by:

`x ' (t) = -9*cos ((\pi *t)/(6))*sin ((\pi √(t + 1) )/(2))`

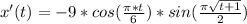
- The slope of the curve at point B, in mathematical terms that is called the inflection point.

- The independent variable time (t) can be determined for the particle when it is at point B. Where the x'(t) is set to zero, and the critical value defines the point B.

`x ' (t) = -9*cos ((\pi *t)/(6))*sin ((\pi √(t + 1) )/(2)) = 0\\\\cos ((\pi *t)/(6)) = 0 , sin ((\pi √(t + 1) )/(2)) = 0\\\\(\pi *t)/(6) = (\pi )/(2) , (\pi √(t + 1) )/(2) = \pi \\\\t = 3 , t = 3`

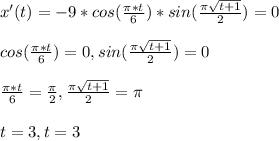
- Hence, the particle is at point B at t = 3 s.