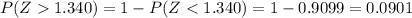Question

Suppose a large shipment of microwave ovens contained 12% defectives. If a sample of size 474 is selected, what is the probability that the sample proportion will be greater than 14%

Answer 1

`P(\hat p>0.14)`

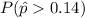
And using the z score given by:

`z = (\hat p -\mu_p)/(\sigma_p)`

Where:

`\mu_(\hat p) = 0.12`

`\sigma_(\hat p)= \sqrt{(0.12*(1-0.12))/(474)}= 0.0149`

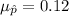
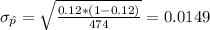
If we find the z score for
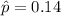`\hat p =0.14` we got:

`z = (0.14-0.12)/(0.0149)= 1.340`

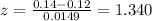
So we want to find this probability:

`P(z>1.340)`

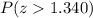
And using the complement rule and the normal standard distribution and excel we got:

`P(Z>1.340) = 1-P(Z<1.340) = 1-0.9099= 0.0901`

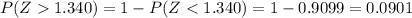
Explanation:

For this case we have the proportion of interest given
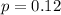`p =0.12`. And we have a sample size selected n = 474

The distribution of
`\hat p` is given by:

`\hat p \sim N (p , \sqrt{(p(1-p))/(n)})`

We want to find this probability:

`P(\hat p>0.14)`

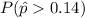
And using the z score given by:

`z = (\hat p -\mu_p)/(\sigma_p)`

Where:

`\mu_(\hat p) = 0.12`

`\sigma_(\hat p)= \sqrt{(0.12*(1-0.12))/(474)}= 0.0149`

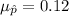
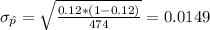
If we find the z score for
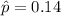`\hat p =0.14` we got:

`z = (0.14-0.12)/(0.0149)= 1.340`

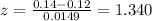
So we want to find this probability:

`P(z>1.340)`

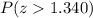
And using the complement rule and the normal standard distribution and excel we got:

`P(Z>1.340) = 1-P(Z<1.340) = 1-0.9099= 0.0901`