Question

Suppose a large consignment of cell phones contained 19% defectives. If a sample of size 399 is selected, what is the probability that the sample proportion will differ from the population proportion by more than 5%

Answer 1

0.88% probability that the sample proportion will differ from the population proportion by more than 5%

Explanation:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

For proportions p in a sample of size n, we have that
`\mu = p, \sigma = \sqrt{(p(1-p))/(n)}`

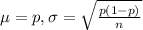
In this problem:

`\mu = 0.19, \sigma = \sqrt{(0.19*0.81)/(399)} = 0.0191`

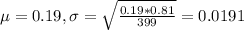
What is the probability that the sample proportion will differ from the population proportion by more than 5%?

Less than 0.19 - 0.05 = 0.14 or greater than 0.19 + 0.04 = 0.24. Since the normal distribution is symmetric these probabilities are equal, which means that we can find one of them and multiply by 2. So

Probability of being less than 0.14.

pvalue of Z when X = 0.14. So

`Z = (X - \mu)/(\sigma)`

`Z = (0.14 - 0.19)/(0.0191)`

`Z = -2.62`

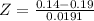
`Z = -2.62` has a pvalue of 0.0044

2*0.0044 = 0.0088

0.88% probability that the sample proportion will differ from the population proportion by more than 5%