Answer:
The distance of the boat from the edge of the cliff is 655.75 ft
Distance of the boat from the base of the cliff is 251.72 ft
Explanation:
Height of person above sea level = 235 ft
Angle of depression of sight to the boat from the person = 21°
Therefore, based on similar angle between person and angle of depression and the boat with angle of elevation we have,
Angle of elevation of the location of the person as sighted from the boat θ = 21°
Distance from the edge of the cliff of the boat is then given by;

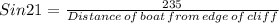
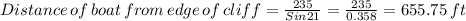
Distance of the boat from the base of the cliff is given by
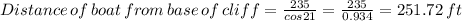 .
.