Question

Suppose the depth of a lake can be described by the function y = 323(0.976)x, where x represents the number of weeks from today. Today, the depth of the lake is 323 ft. What will the depth be in 6 weeks? Round your answer to the nearest whole number. The depth of the lake will be ft. in 6 weeks

Answer 1

The dept of the lake will be 279 ft in 6 weeks

Explanation:

We are given that the depth of a lake can be modeled by the function

`y = 323(0.976)^(x)`

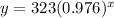
Where x is the number of weeks and y is the depth of lake in feet

The depth of the lake today is (x=0)

`y = 323(0.976)^(0)`

`y=323`
`ft`

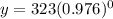
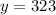
The depth of the lake after 6 weeks will be (x=6)

`y = 323(0.976)^(6)`

`y = 323(0.864)`

`y=279`
`ft`

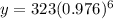
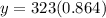
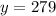
Therefore, the dept of the lake will be 279 ft in 6 weeks.