Given:
Given that ten years ago a collector paid $2000 for a Cal Ripkin autographed baseball. Today it is worth $24,000.
We need to determine the annual rate of appreciation.
Rate of appreciation:
The rate of appreciation can be determined using the formula,
![r=100[((A)/(P))^{(1)/(t)}-1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/o64mzth1uouas2nrfuawwvxuv9rvrih7dk.png)
where A is the total amount,
P is the initial amount,
t is the time in years and
r is the rate of appreciation.
Substituting A = 24,000, P = 2000 and t = 10, we get;
![r=100[((24000)/(2000))^{(1)/(10)}-1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/p0ltdqrg0992wv8eifhq874ab2u4td3vss.png)
Simplifying, we get;
![r=100[(12)^{(1)/(10)}-1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/bgesvx8p19fvjjfm672egm3lvsqgjw5790.png)
![r=100[(1.28209)-1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/mck670aiz0ds612rnn9plhqayofdn22cz5.png)

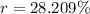
Thus, the rate of appreciation is 28.209%