Question

A review of 200 days-away-from-work injuries for a large, multi-facility corporation was conducted, and it was determined that 18 of them were due to lower back injuries. Only 14.3 were expected under normal conditions. The rest of the injuries were due to other causes where 185.7 were expected. What is the chi-square value? Discuss whether there was a significant difference in observed data vs. the expected data. Also, discuss how the process of hypothesis testing might prove helpful to the safety professional.

Answer 1

a) Chi square value = 1.031

b) There is no significant difference between the observed and expected values.

c) Check explanations for the part C of the question

Explanation:

a) People away from work due to lower back injuries:

Observed value = 18

Expected value = 14.3

People away from work due to other injuries:

Observed value = 200 - 18 = 182

Expected value = 185.7

The chi square value is calculated by the formula:

`x^(2) = ((O-E)^(2) )/(E)`

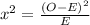
For people out of work due to lower back injuries:

Chi square value,

`x^(2) = ((18-14.3)^(2) )/(14.3) \\x^(2) = 0.957`

For people out of work due to other injuries:

Chi square value,

`x^(2) = ((182-185.7)^(2) )/(185.7) \\x^(2) = 0.074`

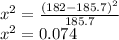
Total chi square value for the distribution:

`x^(2) = 0.074 + 0.957\\x^(2) = 1.031`

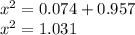
b) The degree of freedom, df = n -1

n = 2 ( two categories of people are considered)

df = 2-1 = 1

For df = 1 and, chi square = 1.031

P - value = 0.3099

p- value = 0.3099, the result is not significant at p < 0.05

There is no significant difference between the observed and expected values.

c) Hypothesis testing helps the safety professionals to statistically analyse any situations and determine whether or not they are safe. It can help them to predict the outcome of a given situation by making necessary observations.