Answer:
108 cubes
Explanation:
Lengths of one of the cube s=

Volume of a Cube
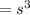
Volume of one of the Cubes
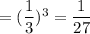
The volume of the rectangular prism is 4 cubic units.
Therefore, to find the number of cubes it takes to fill the prism, we divide the volume of the prism by the volume of the cube.
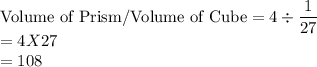
It takes 108 cubes to fill the rectangular prism.