Question

Calculate the area of the shaded region in each figure. Use 3.14 and round to the nearest tenth, if necessary.

Answer 1

Given:

A larger circle consisting of two circles with radii of 4 cm and 8 cm each.

To find:

The area of the shaded region.

Solution:

The centers of the circles with radii 4 cm and 8 cm lie on the same line as the center of the larger circle.

So the diameter of the outer circle
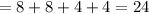`= 8+8+4+4=24` cm.

If the diameter is 24 cm, the radius is
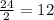`(24)/(2) =12` cm.

The area of the shaded region is obtained by subtracting the areas of the two inner circles from the outer circle.

The area of a circle
`= \pi r^(2) .`

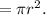
The area of the circle with radius 12 cm
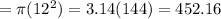`= \pi (12^(2)) = 3.14(144) = 452.16` square cm.

The area of the circle with radius 8 cm
`= \pi (8^(2)) = 3.14(64) = 200.96` square cm.

The area of the circle with radius 4 cm
`= \pi (4^(2)) = 3.14(16) = 50.24` square cm.

The area of the shaded region
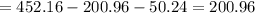`= 452.16-200.96-50.24 = 200.96` square cm.

Rounding this off to the nearest tenth, we get the area of the shaded region as 201 square cm.