Answer:
2/9
Explanation:
The sum of two numbers is 5/9 can be expressed as:
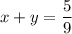
One of the numbers is 1/3. Find the other - this means that either x or y is 1/3 but that doesn’t matter as we can either let x = 1/3 or y = 1/3 via property:
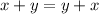
Hence, let x = 1/3:
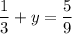
Solve for y - subtract both sides by 1/3:
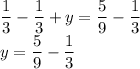
We know that we can only evaluate the fractions if both have same denominator so what we have to do is to multiply 1/3 by 3 for both top and bottom:
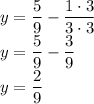
Therefore, the other number is 2/9