Question

The sum of two numbers is 5/9.if one of the numbers is 1/3 find the other

Answer 1

The other number is 2/9

Explanation:

"a" is the other number

The equation:

`a+(1)/(3) =(5)/(9)`

Then

`a=(5)/(9) -(1)/(3) =(15-9)/(27) =(6)/(27)`

simplifying the fraction:

`a = (2)/(9)`

Hope this helps

Answer 2

2/9

Explanation:

The sum of two numbers is 5/9 can be expressed as:

`\displaystyle \large{x+y=(5)/(9)}`

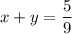
One of the numbers is 1/3. Find the other - this means that either x or y is 1/3 but that doesn’t matter as we can either let x = 1/3 or y = 1/3 via property:

`\displaystyle \large{x+y = y+x}`

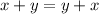
Hence, let x = 1/3:

`\displaystyle \large{(1)/(3)+y=(5)/(9)}`

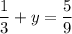
Solve for y - subtract both sides by 1/3:

`\displaystyle \large{(1)/(3)-(1)/(3)+y=(5)/(9)-(1)/(3)}\\\displaystyle \large{y=(5)/(9)-(1)/(3)}`

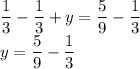
We know that we can only evaluate the fractions if both have same denominator so what we have to do is to multiply 1/3 by 3 for both top and bottom:

`\displaystyle \large{y=(5)/(9)-(1\cdot 3)/(3\cdot 3)}\\\displaystyle \large{y=(5)/(9)-(3)/(9)}\\\displaystyle \large{y=(2)/(9)}`

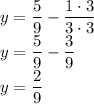
Therefore, the other number is 2/9