Question

The 20-g bullet is traveling at 400 m>s when it becomes embedded in the 2-kg stationary block. Determine the distance the block will slide before it stops. The coefficient of kinetic friction between the block and the plane is mk = 0.2.

Answer 1

distance = 4 m

Step-by-step explanation:

given data

mass of bullet = 20 gm

velocity = 400 m/s

mass of stationary block = 2 kg

coefficient of kinetic friction = 0.2

solution

we will use here law of conservation of linear momentum

Momentum before collision = Momentum after collision ...............1

here

Momentum before collision = (0.02 × 400) + 0 (stationary block)

solve we get

momentum before collision = 8 kg m/s

and

Momentum after collision = (2 + 0.02) v

put here value and we get

8 = 2.02 × v

v = 3.96 m/s.

so

as per work-energy theorem say that

KE of the block + bullet system = work done by Friction to stop motion of the block + bullet system ..........................2

put here value and we get

Kinetic energy = 0.5 × (2.02) × (3.96²)

Kinetic energy = 15.84 J

and

Work done by the frictional force is express as

Work done = F × (distance moved by the force) ......................3

put here value and we get

F = μ × mg

F = 0.2 × (2.02) × (9.8)

F = 3.96 N

and

distance will be

3.96 d = 15.84

distance d =
`(15.84)/(3.96)`

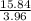
distance = 4 m