Question

Depth d (in feet) of a river can be modeled by the equation d=−0.25t2+1.7t+3.5, where 0≤t≤7 and t is the time (in hours) after a heavy rain begins. When is the river 6 feet deep?

Answer 1

The river is 6 feet at two times, 2.15 hours after the rain and 4.65 hours after the rain.

Explanation:

We are given the following in the question:

`d=-0.25t^2+1.7t+3.5`

`0\leq t\leq 7`

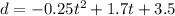
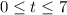
where, d is the depth of river in feet and t is time in hours after a heavy rain.

We have to find the number of hours for which the depth of river is 6 feet.

Putting d = 6 in the equation, we get,

`6=-0.25t^2+1.7t+3.5\\\Rightarrow +0.25t^2-1.7t+2.5 = 0\\\text{Using quadratic formula}\\\\\Rightarrow t = (1.7\pm √((-1.7)^2-4(0.25)(2.5)))/(2(0.25))\\\\t\approx 4.65, 2.15`

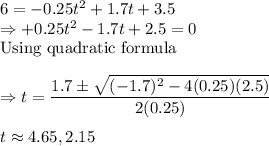
Thus, the river is 6 feet at two times, 2.115 hours after the rain and 4.65 hours after the rain.

The attached image shows the graph.