Question

Two similar cylinders have surface areas of 24 cm2 and 54 cm2. The volume of the smaller cylinder is 16 cm2.

What is the volume of the larger cylinder?

Answer 1

54π cm³

Explanation:

Answer 2

Given:

Given that two similar cylinder have surface areas 24π cm² and 54π cm².

The volume of the smaller cylinder is 16π cm³

We need to determine the volume of the larger cylinder.

Volume of the larger cylinder:

The ratio of the two similar cylinders having surface area of 24π cm² and 54π cm², we have;

`(24 \pi)/(54 \ pi)=(4)/(9)`

`=(2^2)/(3^2)`

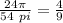
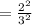
Thus, the ratio of the surface area of the two cylinders is
`(2^2)/(3^2)`

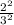
The volume of the larger cylinder is given by

`(2^2)/(3^2)* (2)/(3)=(16 \pi )/(x)`

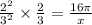
where x represents the volume of the larger cylinder.

Simplifying, we get;

`(2^3)/(3^3)=(16 \pi )/(x)`

`(8)/(27)=(16 \pi )/(x)`

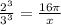
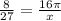
Cross multiplying, we get;

`8x=16 \pi * 27`

`8x=432 \pi`

`x=54 \pi \ cm^3`

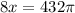
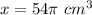
Thus, the volume of the larger cylinder is 54π cm³