Answer:
Option b)
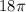 is correct
is correct
∴ the volume of the solid is
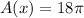 cubic units
cubic units
Explanation:
Given that the base of a solid is the circle
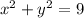 and Cross sections of the solid perpendicular to the x-axis are semi-circles.
and Cross sections of the solid perpendicular to the x-axis are semi-circles.
To find the the volume of the solid in cubic units:
We know that the cross sections are semicircles with the diameter in the given circle
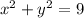
That is we have to find the formula for the area of any semicircle perpendicular to x-axis, and integrate it from -3 to 3.
Now the area of a semicircle is
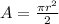 cubic units
cubic units
Let r = y and
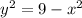
Then area of the semicircle crossing the x-axis at x is given by
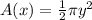 cubic units
cubic units
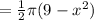
Now we can find the definite integral of A(x) from x = -3 to x = 3.
Since A(x) is an EVEN function then the definite integral of A(x) from x = -3 to x = 3 is the same as twice the integral of A(x) from x = 0 to x = 3.
We have that
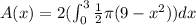
![=2((\pi)/(2)[9x-(x^3)/(3)]_0^3)](https://img.qammunity.org/2021/formulas/mathematics/high-school/qnyusrxc0ngau7ydfp1yugmjiz9y4a8xgr.png)
![=\pi[9(3)-(3^3)/(3)-9(0)-(-(0^3)/(3))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/uglgdip42l8uschus0qsv71jr6o5amgjji.png)
![=\pi[27-(27)/(3)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/zp0zt2yikmlgj7zzequ7wdpxt4olfksidl.png)
![=\pi[27-9]](https://img.qammunity.org/2021/formulas/mathematics/high-school/sfpg8iff4cj27jx2x3f3lkjkx17fjdyx5n.png)
![=\pi[18]](https://img.qammunity.org/2021/formulas/mathematics/high-school/8xf4ri90pt5rb5ddhlk706xosqqb2d5jwh.png)
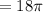
∴ option b)
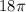 is correct
is correct
∴ the volume of the solid is
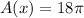 cubic units
cubic units