Given Information:
Sample size = n = 40
sample proportion = p = 35% = 0.35
Required Information:
standard deviation of sample proportion = σ
Answer:
standard deviation of sample proportion = σ = 0.075
Step-by-step explanation:
Check if the condition np ≥ 10 or n(1 - p) ≥ 10 is satisfied
np ≥ 10
40*0.35 ≥ 10
14 ≥ 10 satisfied
n(1 - p) ≥ 10
40(1 - 0.35) ≥ 10
26 ≥ 10 satisfied
Which means that distribution of sample proportion will have a mean closer to the population proportion.
The standard deviation for sample proportion is given by
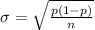
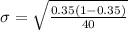
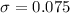
Therefore, the standard deviation for the sampling distribution of the sample proportions is 0.075.