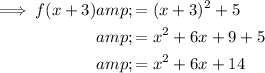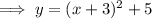Answer:
1)

2)
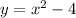
3)
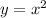
4)
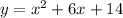
Explanation:
Question 1
Given points: (-2, 6) (-1, 3) (0, 2) (1, 3)
This is likely to be a quadratic equation with a vertex of (0, 2) since the points (-1, 3) and (1, 3) are symmetrical about x = 0
Vertex form of quadratic equation:

(where (h, k) is the vertex)
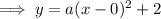
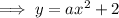
To find a, input one of the points into the equation:
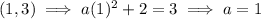
Therefore, the equation of the graph is

Question 2
If the parabola intersects the x-axis at (-2, 0) and (2, 0) then
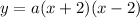
We are told that the y-intercepts if (0, -4). Input this into the equation to find a:
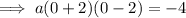
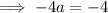
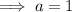
Therefore,
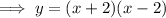

Question 3
Given points: (-2, 4) (-1, 1) (0, 0) (1, 1)
This is likely to be a quadratic equation with a vertex of (0, 0) since the points (-1, 1) and (1, 1) are symmetrical about x = 0
Vertex form of quadratic equation:

(where (h, k) is the vertex)
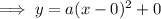

To find a, input one of the points into the equation:
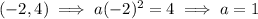
Therefore, the equation of the graph is
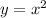
Question 4
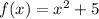
If we wish to move the function to the left by 3 units, we substitute x for
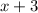 :
: