Question

The inside diameter of a randomly selected piston ring is a random variable with mean value 16 cm and standard deviation 0.05 cm. Suppose the distribution of the diameter is normal. (Round your answers to four decimal places.) Calculate P(15.99 ≤ X ≤ 16.01) when n = 25.

Answer 1

P(15.99 ≤ X ≤ 16.01) = 0.1586

Explanation:

Explanation:-

Step(i):-

Given data the inside diameter of a randomly selected piston ring is a random variable with mean value 16 cm and standard deviation 0.05 cm.

The mean of the Population 'μ' = 16cm

The standard deviation of the Population 'σ' = 0.05cm

Given 'X' be the Normal Variable

(i) Given X = 15.99

`Z _(1) = (x-mean)/(S.D) = (15.99-16)/(0.05) = -0.2<0`

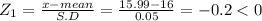
(ii) Given X = 16.01

`Z_(2) = (x-mean)/(S.D) = (16.01-16)/(0.05) = 0.2>0`

Step(ii):-

P(x₁ ≤ X ≤ x₂) = A(z₂)+A(z₁)

P(15.99 ≤ X ≤ 16.01)= P(-0.2≤ z ≤ 0.2) = A(z₂)+A(z₁)

= A(0.2)+A(-0.2) [ A(-Z) = A(Z)]

= 0.0793 + 0.0793

= 0.1586

Conclusion:-

P(15.99 ≤ X ≤ 16.01) = 0.1586