Question

An ant arrives at the snail’s starting position at time minutes and follows the snail’s path. During the interval minutes, the ant travels in the same direction as the snail with a constant acceleration of 2 inches per minute per minute. The ant catches up to the snail at time minutes. The ant’s velocity at time is B inches per minute. Find the value of B.

Answer 1

QUESTION BEGINNING

Given a snail is traveling along a straight path. The snail’s velocity can be modeled by
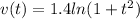`v(t)=1.4ln(1+t^2)` inches per minute for 0 ≤ t ≤ 15 minutes.

Answer:

B=22.35 Inches per minutes

Explanation:

If the snail's velocity is
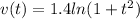`v(t)=1.4ln(1+t^2)` per minute, its displacement for 0 ≤ t ≤ 15 minutes is given by the integral:

`\int v(t) dt=\int (1.4ln(1+t^2))dt=76.04307`

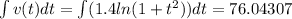
The constant acceleration of the ant is 2 Inches per minute.

The velocity of the ant therefore, twill be:

`\int 2 dt=2t+K, $where K is a constant of integration$`

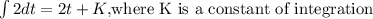
For the interval, 12≤t≤15, the displacement of the ant is:

`\int_(12)^(15)(2t+K) dt=81+3K`

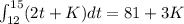
Since the snails displacement and that of the ant are equal in 12≤t≤15.

81+3K=76.04307

3K=76.04307-81

3K=-4.95693

K=-1.65231

At t=12, the velocity of the ant is therefore:

2t+K=2(12)-1.65231=22.348 Inches per minutes

B=22.348 Inches per minutes