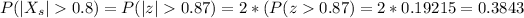Question

The mean weight of an adult is 6060 kilograms with a variance of 100100. If 118118 adults are randomly selected, what is the probability that the sample mean would differ from the population mean by greater than 0.80.8 kilograms? Round your answer to four decimal places.

Answer 1

The probability that the sample mean would differ from the population mean by greater than 0.8 kg is P=0.3843.

Explanation:

We have a population with mean 60 kg and a variance of 100 kg.

We take a sample of n=118 individuals and we want to calculate the probability that the sample mean will differ more than 0.8 from the population mean.

This can be calculated using the properties of the sampling distribution, and calculating the z-score taking into account the sample size.

The sampling distribution mean is equal to the population mean.

`\mu_s=\mu=60`

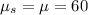
The standard deviation of the sampling distribution is equal to:

`\sigma_s=\sigma/√(n)=√(100)/√(118)=10/10.86=0.92`

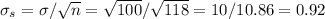
We have to calculate the probability P(|Xs|>0.8). The z-scores for this can be calculated as:

`z=(X-\mu_s)/\sigma_s=\pm0.8/0.92=\pm0.87`

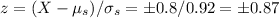
Then, we have:

`P(|X_s|>0.8)=P(|z|>0.87)=2*(P(z>0.87)=2*0.19215=0.3843`