Question

The mean ACT composite score in a recent year is 20.8 with a standard deviation of 5.6. A random sample of 36 ACT composite scores are selected. What is the probability that the mean score for the sample is (a) less than 21.6

Answer 1

0.3051

Step-by-step explanation:

mean (μ) = 20.8, standard deviation (σ) = 5.6 and the number of samples (n) = 36 scores.

Z score also known as standard score is used in probability to measure the number of standard deviations by which the value of what is being measured is above or below the mean. It is given by the equation:

Z score (z) =
`(x-\mu)/((\sigma)/(√(n) ) )`

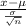
For x = 21.6,

`z=(x-\mu)/((\sigma)/(√(n) ) ) =(21.6-20.8)/((5.6)/(√(36) ) ) =0.86`

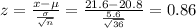
From the probability table:

P(x < 21.6) = P(z < 0.86) = 0.3051 = 30.51%

The probability that the mean score for the sample is less than 21.6 = 30.51%