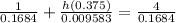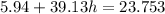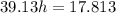Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
The largest offset that can be used is

Step-by-step explanation:
From the question we are told that
The diameter of the metal tube is
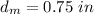
The thickness of the wall is
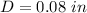
Generally the inner diameter is mathematically evaluated as
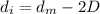

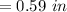
Generally the tube's cross-sectional area can be evaluated as
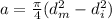
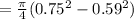
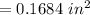
Generally the maximum stress of the metal is mathematically evaluated as
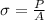
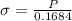
The diagram showing when the stress is been applied is shown on the second uploaded image
Since the internal forces in the cross section are the same with the force P and the bending couple M then
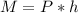
Where h is the offset
The maximum stress becomes

Where
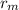 is the radius of the outer diameter which is evaluated as
is the radius of the outer diameter which is evaluated as
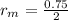
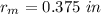
and I is the moment of inertia which is evaluated as
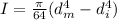
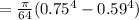

So the maximum stress becomes
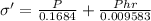
Now the question made us to understand that the maximum stress when the offset was introduced must not exceed the 4 times the original stress
So
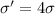
=>
![(P)/(0.1684) + (Phr_m )/(0.009583) = 4 [(P)/(0.1684) ]](https://img.qammunity.org/2021/formulas/engineering/college/4wj1t1deiin07kjbbxofslm3l0jtvu608p.png)
The P would cancel out