Question

An electron follows a helical path in a uniform magnetic field given by:B =(20i^−50j^−30k^)mTAt time t = 0, the electron's velocity is given by:⃗v=(40i^−30j^+50k^)m/sa. What is the angle ϕ between v and B. The electron's velocity changes with time. Do b. its speed c. the angled. What is the radius of the helical path?

Answer 1

a) 1.38°

b) 7.53*10^11 m/s/s

c) 6.52*10^-9m

Step-by-step explanation:

a) to find the angle you can use the dot product between two vectors:

`\vec{v}\cdot\vec{B}=vBcos\theta\\\\\theta=cos^(1)(\frac{\vec{v}\cdot\vec{B}}{vB})`

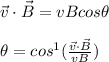
v: velocity of the electron

B: magnetic field

By calculating the norm of the vectors and the dot product and by replacing you obtain:

`B=√((20)^2+(50)^2+(30)^2)=61.64mT\\\\v=√((40)^2+(30)^2+(50)^2)=70.71m/s\\\\\vec{v}\cdot\vec{B}=[(20)(40)+(50)(30)-(30)(50)]mTm/s=800mTm/s\\\\\theta=cos^(-1)((800*10^(-3)Tm/s)/((70.71m/s)(61.64*10^(-3)T)))=cos^(-1)(0.183)=1.38\°`

the angle between v and B vectors is 1.38°

b) the change in the speed of the electron can be calculated by the change in the momentum in the following way:

`(dp)/(dt)=F_e=qvBsin\theta\\\\(dp)/(dt)=(1.6*10^(-19)C)(70.71m/s)(61.64*10^(-3)T)(sin(1.38\°))=6.85*10^(-19)N`

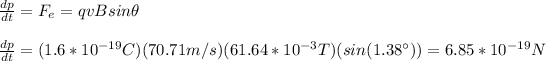
due to the mass of the electron is a constant you have:

`(dp)/(dt)=(mdv)/(dt)=6.85*10^(-19)N\\\\(dv)/(dt)=(6.85*10^(-19)N)/(9.1*10^(-31)kg)=7.53*10^(11)(m/s)/s`

the change in the speed is 7.53*10^{11}m/s/s

c) the radius of the helical path is given by:

`r=(m_ev)/(qB)=((9.1*10^(-31)kg)(70.71m/s))/((1.6*10^(-19)C)(61.64*10^(-3)T))=6.52*10^(-9)m`

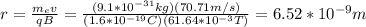
the radius is 6.52*10^{-9}m