Answer:
Part (a)
Given quadratic:
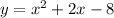
Factored form
To factor, find two numbers that multiply to -8 and sum to 2: 4 and -2
Rewrite the middle term of the quadratic as the sum of these number:
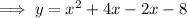
Factorize the first two terms and the last two terms separately:
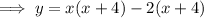
Factor out the common term
 :
:
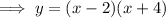
Zeros
The zeros of the quadratic polynomial are the x-coordinates of the points where the graph intersects the x-axis, i.e. when y = 0
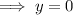
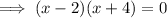
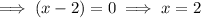
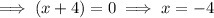
Therefore, the zeros are 2 and -4
Vertex
The x-coordinate of the vertex is the midpoint of the zeros.
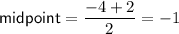
To find the y-coordinate of the vertex, substitute the found value of x into the given equation:
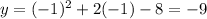
Therefore, the vertex is (1, -9)
------------------------------------------------------------------------------------------------
Part (b)
Given quadratic:
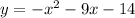
Factored form
To factor, first factor out -1:
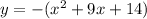
Now find two numbers that multiply to 14 and sum to 9: 7 and 2
Rewrite the middle term of the quadratic as the sum of these number:

Factorize the first two terms and the last two terms separately:
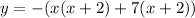
Factor out the common term
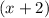 :
:
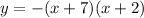
Zeros
The zeros of the quadratic polynomial are the x-coordinates of the points where the graph intersects the x-axis, i.e. when y = 0
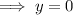
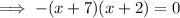
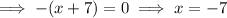

Therefore, the zeros are -7 and -2
Vertex
The x-coordinate of the vertex is the midpoint of the zeros.
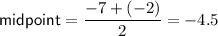
To find the y-coordinate of the vertex, substitute the found value of x into the given equation:
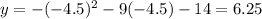
Therefore, the vertex is (-4.5, 6.25)