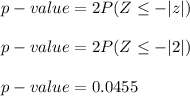Question

The quality-control manager at a compact fluorescent light bulb factory need to determine whether the mean life of a large shipment of bulbs is equal to 7,500 hours. The population standard deviation is 1,000 hours. A random sample of 64 bulbs indicates a sample mean life of 7,250 hours. 1. Set the hypothesis, for matching this statement "Is there evidence that the mean life is difference from 7,500 hours?" 2. At 95% confidence, what is the estimation of population mean life of the bulbs? 3. Compute p-value. 4. Find the solution, by using level of significance = 0.05

Answer 1

Complete Question:

The mean life of a large shipment of CFLs is equal to 7,500 hours. The population standard deviation is 1,000 hours. A random sample of 64 CFLs indicate a sample life of 7,250 hours.

1. State the Null and Alternative Hypothesis.

2. At the 0.05 level of significance, is there evidence that mean life is different from 7,500 hours.

3. Construct a 95% confidence interval estimate of the population mean life of the CFLs.

4. Compute the p-value and interpret its meaning.

Answer:

-2, (7005, 7450), 0.045

Step-by-step explanation:

1).

H₀: mean of life shipment is 7500 hours

the hypothesis are outlined as follows

H₀:
`\mu =` 7500

H₁:
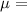`\mu \\eq` 7500

where, n = 64, x = 7250,
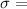`\sigma =`1000 hours

Test statistics:

`Z = (7250-7500)/((1000)/(√(64)) ) \\\\Z = -2`

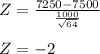
Our conclusion from the above result is that there is sufficient evidence to say that the mean life is different from 7500 hours

2). 95% confidence Interval for the population mean
`\mu` is

`[7250-1.96* (1000)/(√(64)),7250+1.96* (1000)/(√(64)) ]\\\\(7005,7495)`

3).

the p-value is given by

`p-value =2P(Z\leq -|z|)\\\\p-value =2P(Z\leq -|2|)\\\\p-value = 0.0455`