Question

At Robin's Snow Cones, the shaved ice portion of the cone is shaped like a perfect sphere with a diameter of 8 cm. Exactly half of the shaved ice sphere extends above the paper cup holder. What is the volume of ice that extends above the cup to the nearest cubic centimeter? In your calculations, use LaTeX: \pi\:=\:3.14

Answer 1

The extended volume of hemisphere to nearest cubic centimeter is V = 134 cm^3

Explanation:

Solution:-

- The shaved ice is modeled as a sphere.

- The half of the shaved ice sphere extends above the cup holder.

- The volume of sphere with radius r = diameter d / 2 :

`V = (4)/(3)*\pi *r^3`

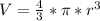
- We are to calculate the volume of the extended part of the sphere with diameter d = 8 cm or radius r = 4 cm.

- The volume of hemisphere is:

`V = (1)/(2) *(4)/(3)*3.14 *r^3= (2)/(3)*3.14 *r^3\\\\V = (2)/(3)*3.14 *4^3 \\\\V =134.04128 cm^3`

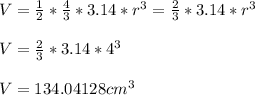
- The extended volume of hemisphere to nearest cubic centimeter is V = 134 cm^3