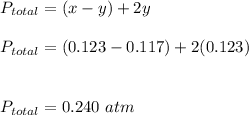Question

At 5000 K and 1.000 atm, 83.00% of the oxygen molecules in a sample have dissociated to atomic oxygen. At what pressure will 95.0% of the molecules dissociate at this temperature

Answer 1

At
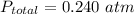`P_(total) = 0.240\ atm`; 95.0% of the molecules will dissociate at this temperature

Step-by-step explanation:

The chemical reaction of this dissociation is:

`O_2 \leftrightarrow 2O_g`

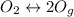
The ICE table is as follows:

`O_2 \ \ \ \ \ \ \ \leftrightarrow \ \ \ \ \ \ \ \ 2O_g`

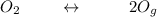
Initial 100 0

Change -83 +166

Equilibrium 17 166

The mole fractions of each constituent is now calculated as:

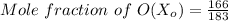`Mole \ fraction \ of \ O(X_o) = (166)/(183)` = 0.9071

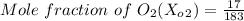`Mole \ fraction \ of \ O_2(X_o_2_}}) = (17)/(183)` = 0.0929

Given that the total pressure
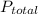`P_(total)` = 1.000 atm ; the partial pressure of each gas is calculated by using Raoult's Law.

`Partial \ Pressure \ of \ O (P_o) = X_oP_(total)\\\\ = 0.9071 \ atm`

`Partial \ Pressure \ of \ O_2 (P_o_2) = X_oP_(total)\\\\ = 0.0929 \ atm`

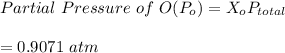
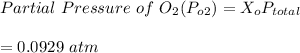
Now; we proceed to determine the equilibrium constant
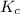`K_c`; which is illustrated as:

`K_c = (Po^2)/(Po_2) \\ \\ K_c = ((0.9072)^2)/(0.0929) \\ \\ =8.86 \ atm`

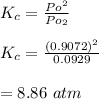
Let assume that the partial pressure of
`O_2` be x ;&

the change in pressure of
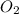`O_2` be y ; then

we can write that the following as the changes in concentration of species :

`O_2 \ \ \ \ \ \ \ \leftrightarrow \ \ \ \ \ \ \ \ 2O_g`

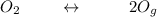
Initial x 0

Change -y +2 y

Equilibrium x - y 2 y

From above; we can rewrite our equilibrium constant as:

`K_c = ((2y)^2)/(x-y) \\ \\ 8.86 = ((2y)^2)/(x-y) ----- equation (1)`

From the question; we are told that provided that 95% of the molecules dissociate at this temperature. Therefore, we have:

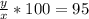`(y)/(x)*100 = 95`% -------- equation (2)

Solving and equating equation 1 and 2 ;

x = 0.123 atm

y = 0.117 atm

Thus, the pressure required can be calculated as :

`P_(total) = (x-y) +2y \\ \\ P_(total) = (0.123- 0.117)+ 2(0.123) \\ \\ \\ P_(total) = 0.240 \ atm`