Answer:
18.83% (nearest hundredth)
Explanation:
Continuous Compounding Formula
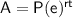
where:
- A = amount
- P = principal (initial amount)
- e = mathematical constant ≈ 2.7183
- r = interest rate (in decimal form)
- t = time in years
Given:
- A = $1,300
- P = $420
- t = 6 years
Substituting given values into the formula:
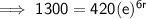
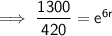
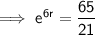
Taking natural logs of both sides:

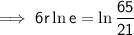
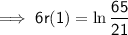
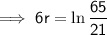
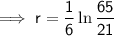
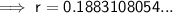
Therefore, the interest rate is 18.83% (nearest hundredth)