Question

The true absorbance for a 1.0 x 10 −5 M solution is 0.7526. If the percentage stray light for a spectrophotometer is 0.56%, calculate the percentage by which the apparent concentration deviates from the known concentration.

Answer 1

The percentage deviation is
`\Delta M = 1.87`%

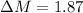Step-by-step explanation:

From the question we are told that

The concentration is of the solution is
`C = 1.0*10^(-5) M`

The true absorbance A = 0.7526

The percentage of transmittance due to stray light
`z = 0.56`%
`=(0.56)/(100) = 0.0056`

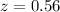Generally Absorbance is mathematically represented as

`A = -log T`

Where T is the percentage of true transmittance

Substituting value

`0.7526 = - log T`

`T = 10^(-0.7526)`

`= 0.177`

`= 17.7`%

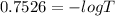
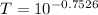
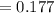
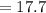The Apparent absorbance is mathematically represented

`A_p = -log (T +z)`

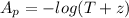
Substituting values

`A_p = -log(0.177 + 0.0056)`

`= -log(0.1826)`

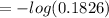
= 0.7385

The percentage by which apparent absorbance deviates from known absorbance is mathematically evaluated as

`\Delta A = (A -A_p)/(A) * (100)/(1)`

`= (0.7526 - 0.7385)/(0.7526) * (100)/(1)`

`\Delta A = 1.87`%

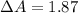Since Absorbance varies directly with concentration the percentage deviation of the apparent concentration from know concentration is

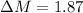`\Delta M = 1.87`%