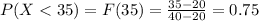Question

The thickness of a protective coating applied to a conductor designed to work in corrosive conditions follows a uniform distribution over the interval [20,40] microns. a. Find the mean and standard deviation of the thickness of the protective coating. b. Find also the probability that the coating is less than 35 microns thick

Answer 1

Answer: it's 6.3

Explanation:

Answer 2

a) For this case the mean is given by:

`E(X) = (a+b)/(2)= (20+40)/(2)= 35`

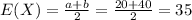
The variance is given by:

`Var(X) = ((b-a)^2)/(12)= ((40-20)^2)/(12) =33.33`

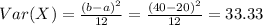
And the deviation would be:

`Sd(X) = √(33.33)= 5.774`

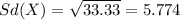
b) For this case we want to find this probability:

`P(X<35)`

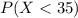
And we can use the cumulative distribution function given by:

`F(X) = (x-a)/(b-a) , a \leq X \leq b`

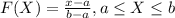
And using this we got:

`P(X<35) = F(35) = (35-20)/(40-20)= 0.75`

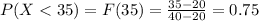
Explanation:

For this case we define the random variable X as the hickness of a protective coating applied to a conductor and we know that the distribution of X is given by:

`X \sim Unif (a= 20, b=40)`

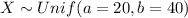
Part a

For this case the mean is given by:

`E(X) = (a+b)/(2)= (20+40)/(2)= 35`

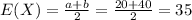
The variance is given by:

`Var(X) = ((b-a)^2)/(12)= ((40-20)^2)/(12) =33.33`

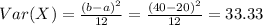
And the deviation would be:

`Sd(X) = √(33.33)= 5.774`

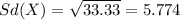
Part b

For this case we want to find this probability:

`P(X<35)`

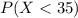
And we can use the cumulative distribution function given by:

`F(X) = (x-a)/(b-a) , a \leq X \leq b`

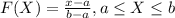
And using this we got:

`P(X<35) = F(35) = (35-20)/(40-20)= 0.75`